ZOJ 1010. Area.
基本題意:此題目給出 n 個點的坐标 (xi,yi ) ,要求求出這些點按順序圍成的多邊形的面積。同時要求檢測出不合法的多邊形(例如非相鄰邊彼此相交的情況)。
此題求面積不難,樣例很容易就過了,但是送出 10+ 次基本都是 WA ,幾乎失去信心。做題最郁悶的就是你不知道問題到底出在什麼地方,可能改了很多次都沒有試對地方。後來跑到 88 的算法版搜了下,看到别人的代碼,然後事後總結實際還是卡在了什麼樣的多邊形是 Impossible 的,這個檢測代碼沒有寫好,耐心不夠導緻。
(1)求面積很簡單,類似求某個曲線的區間積分
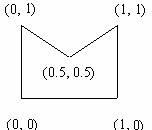
用所有多邊形的邊和X軸圍成的梯形的面積累加起來就可以了。例如某條邊 ( P1 - P2 ) 和在它在 x 軸的投影 ( p1' - P2' ) 所圍成的梯形面積是:
S [ p1->p2 ] = 1/2 * ( y1 + y2 ) * ( x2 - x1 ) ; ----(I)
這個式子拆開後就是:
S [ p1->p2 ] = 1/2 * ( -x1 * y1 + x2 * y2 - x1 * y2 + x2 * y1 ) ; ---- ( 注:藍色部分的 xi * yi 累加後被消掉 )
由于每個邊都被累加一遍,每個點參與了組成邊兩次(前一條邊的終點和後一條邊的起始點),是以每個頂點自身坐标的乘積 ( xi * yi ) 累加的時候都被消掉了!最後就是累加所有的式(I):
Area = ∑ 1/2 * ( -x( i ) * y( i + 1 ) + x( i + 1 ) * y( i ) ) ;
----( i = 1,2,...,n,且P(n+1) = P(0) ); ----(II)
上面的式子,括号内是兩個矢量的叉積 P[ i + 1 ] × P[ i ]。是以式II實際上是依次累加相鄰點的叉積,最後在除以2。考慮叉積的含義,是以兩個矢量為相鄰邊的平行四邊形(由 O(0,0), P1, P2, (P1 + P2) 四個點組成)的面積(在平面坐标中用三角形面積相減可以很容易推導出該含義),是以這個方法的實體意義就非常明顯了,我們可以直覺的假定原點位于多邊形内部,顯然依次把相鄰點和原點圍成的三角形的面積累加起來就是這些點組成的多邊形的面積。是以 1/2 ( P[ i + 1 ] X P[ i ] ) 就是三角形 O - P[ i + 1 ] - P[ i ] 的面積(平行四邊形面積的一半,O 表示原點)。當然,由于叉積有符号,是以原點位于多邊形外部也成立,隻是在内部更直覺,更容易了解。
備注:我們可以把存儲頂點的數組擴充一個元素,然後把 P( n+1 ) 指派為 P( 0 ),這樣我們對上式的循環中就不必對頂點索引使用取模運算(MOD)。我自己寫的代碼采用的(I)這種計算方法,我參考的代碼采用(II)中的計算方法,兩者計算量相差不大,但後者不太直覺,是以我就稍微解釋了下兩者本質是相同的。
注意式(I)中的梯形面積是有符号的,和 P1,P2 的點順序相關( S[ p1->p2 ] = -S[ p2->p1 ] ) ,是以 Area 的符号和頂點順序有關,是以最後别忘了對計算結果求絕對值。
(2)麻煩在于,什麼樣的多邊形是 Impossible 的
做題的時候肯定我們就會着重考慮這一點。因為不管任何多邊形,按照(1)都能算出個面積,但是多邊形是否是有效的需要單獨判斷。設多邊形有 n 個頂點和邊,則:
2.1) n < 3 時,顯然是 Impossible,因為一個點或一個線段不能組成多邊形。
2.2) n > 3 時,依次判斷每條邊 和 它的所有非相鄰邊 不能相交(包含交點位于某一條線段上的情況),保證這一點即可。
2.3) n = 3 時,是三角形,無須做 2.2 中的檢測。如果三角形的三個點共線的話,是不是應該輸出 Impossible,我們沒有考慮也 AC 了 (即我們會對這種情況認為是有效的而輸出 0.00),估計 OL平台的測試輸入也沒有考慮這種情況。
下面我們考慮2.2中的檢測:
總的邊數為 n,則每條邊的非相鄰邊為(n-3)條,是以檢測完所有邊的情況類似冒泡排序,以及繪制多邊形所有頂點的連接配接線的金剛石圖形,需要耗費O(n^2)的時間複雜度。
相鄰邊必然是相交于頂點的是以不用檢測,即使相鄰邊向内重疊了,比如連續的三個頂點:(0,0),(0,5),(0,3)這種情況也不必擔心,因為在下一條邊檢測時也會檢測出相交情況的。
判斷兩個線段是否相交屬于算法中的計算幾何部分,主要原理是 如果兩個線段相交,則從任何一個線段角度看,另一個線段的兩個端點都位于它自己的兩側(該線段以任一端點為原點旋轉到經過另一個線段的兩個端點的時針方向相反)。 兩個矢量的相對旋轉方向利用矢量叉積求出。
我原來還考慮了浮點數和 0 的比較判斷,實際上最後從送出結果發現無需考慮這個問題,直接和 0 比就是了。
(3)對頂點坐标的存儲
為了檢測多邊形是不是Impossible的,就必須要存儲所有頂點的坐标。如果不需要判斷這個,就不需要任何額外的存儲空間。那樣就簡潔多了。當然那樣的話這道題也就毫無任何難度,也失去了對計算幾何的考察點。
我看了我參考的解法,我居然沒有想到像他開一個次元為1000的數組,ft!我是用了一個連結清單來存儲所有的邊。。。。汗。。。(當然應該用STL就可以,我習慣了自己寫連結清單的代碼),是以我的代碼比我參考的那個人的多好多。。。(他的代碼好簡短!)
另外,由于我用連結清單存儲的是線段,相當于每個頂點被我存儲了兩次,是以實際上還是浪費了一倍的堆上記憶體。另外還要加上連結清單使用的指針占用的空間。當然優點是動态記憶體管理相比靜态數組在記憶體的使用上要靈活一些,這就無須多做解釋了。
檢測邊是否相交實際上和那個人的代碼的原理基本一緻,這部分代碼我基本是照着《算法導論》上的僞碼直譯過來的。
我送出的代碼如下:
CODE_ZOJ1010
另附上我參考的代碼:
code_by_dynamic
參考資料:
1. 《算法導論》,第33章(計算幾何學)33.1 節(線段的性質)。