題意:給出下列參數(所有參數均為小于等于1000的正整數),求地鐵列車從一個站點到下一個站點之間的最短時間(精确到 0.1 秒)。
d - 地鐵站之間的距離(米);
m - 列車的最大速度(米 / 秒);
a1 - 最大加速度(絕對值)(米 / 秒^2);
j1 - 最大 jerk (絕對值)(米 / 秒^3).
備注:最後一個條件中的 Jerk 就是加速度對時間的導數:d/dt (a); 相當于列車所受的合力對時間的變化率,該限制條件用于防止車廂内站立的乘客摔倒。
分析:此題的重點在于考察數學和實體基礎,程式設計本身倒不重要。對這道題目,要求求列車運作的最短時間,顯然,列車應該盡可能快的加速到最大速度,然後盡可能快的減速到停止。這個結論是很顯然的。由于這是OnlineJudge 題目,是以我們也不必此結論做嚴格的數學證明。(如果不是這樣,即列車沒有盡可能快的加速,那麼其 v- t 曲線就會位于最佳曲線的下方,為了保證面積相等,則其時間一定要超過最佳曲線)
可以繪制出列車運作的速度曲線 v = v( t ),根據實體知識,上訴條件相當于下清單達式:
∫ v dt = d; (列車走過的距離,即 v( t ) 曲線和橫軸圍成的面積)
v ≤ m;
| d(v)/dt | ≤ a1;
| d^2(v)/dt^2 | ≤ j1;
根據前面的假設,v(t) 在起始階段一定是以最大的 j1 在加速。是以:
(1)全力加速: v(t) = 1/2 * j1 * t^2; 曲線 v 為一段抛物線。設持續時間為 t1;加速度 a = j1 * t;
(2)當到達t1時,假設此時達到了最大加速度 a1。然後保持加速度為 a1 不變,進入勻加速直線運動階段,此時曲線 v 為斜率為 a1 的直線。加速度 a = a1;設持續時間為 t3;
(3)在此速度上繼續加速,但盡全力降低加速速度,直到最大速度 m。曲線 v 依然是抛物線,隻是開口方向相反。持續時間依然為 t1;加速度 a = - j1 * ( t - t1 - t3);
(4)已最大速度 m 進入勻速直線運動。曲線 v 是水準線段,加速度 a = 0;設該段的持續時間為 t2;
(5)全力減速,抛物線,和(3)對稱,持續時間為 t1。
(6)以最大減速速度 -a1 進行勻減速直線運動,斜率為 -a1 的直線線段,和(2)對稱,持續時間為 t3。
(7)繼續全力減速,直到停止在下一個站點,和(1)對稱,持續時間為 t1。
注意上訴過程包含了 4 個含有參數 j1 的抛物線片段,先解釋下 j1 的實體含義,假設列車運作在光滑軌道上,隻受到一個牽引力,則在這些時間段上,牽引力變化的最快,加速度變化的最快(乘客最容易因為慣性發生搖晃)。實體量 Jerk 表示的是加速度變化的速度,根據牛頓第二定律,也就是物體所受合力的變化速度。例如,列車如果正在用最大牽引力進行全力加速,這時候乘客傾向于向後傾倒,乘客需要用很大力氣緊緊抓住車廂内的扶手,為了讓乘客保持穩定,這個牽引力不應該猛然撤去,而應該逐漸減小(相當于上面的曲線片段 3),如果在全力加速時一瞬間撤去牽引力,乘客就會感覺很不穩定很不舒服(現實生活中這種現象很常見,在列車加速時乘客會感覺非常不穩,也就是列車受力的變化速度太快,即 j 太大了,很顯然實際生活中的地鐵是達不到題目中要求的這麼理想化的)。同理,如果列車在靜止狀态或者勻速狀态,牽引力也應該逐漸加大,而不是一瞬間加到最大(這會對列車産生“猛推”效果,造成乘客在車廂内搖晃)。
最大加速度 a1 的實體含義表征的是牽引或者制動時的最大合力,不考慮刹車的話也就相當于發動機的最大輸出牽引力(注:不是功率)。
上訴過程的速度 v(t)曲線如下圖所示(注意:圖形中的背景色表示的僅是片段的實體運動性質,但不代表互相銜接的曲線一定來自相同函數,下面的 case 圖與此相同):
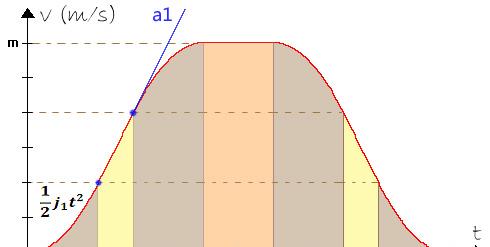
很顯然,曲線是關于垂直中心線軸對稱的。求上訴曲線的積分即和 t 軸圍成的面積很容易,抛物線由四個片段組成,它們能拼合成兩個面積為 (m * t1)的矩形。斜率為 ±a1 的勻加速直線運動部分,是兩個梯形,它們也能拼合成一個面積為 (m * t3)的矩形。最後中間的勻速直線運動部分,是一個面積為(m * t2)的矩形。是以,對于上訴過程有:
d = ∫ v dt = m * ( t1 * 2 + t3 + t2 ); // 兩個站點之間的距離
min ( t ) = t1 * 4 + t3 * 2 + t2; // 最短運作時間
注意:這是一種運動種類最多的“理想狀況”,即距離 d 足夠長,使得可以加速到最大速度 m; a1 要足夠小,使得可以“割斷”抛物線,出現斜線部分。實際上由于四個參數的值是任意給出的整數,這些參數可能隻有一部分真正的對結果産生了限制作用,是以我們必須考慮下面的四種實際 case,如下圖所示:
(1)case 1:受到距離 d 的限制,不受 m,a1 的限制。曲線隻有四個抛物線片段。
根據:∫ v dt = max(v) * t1 * 2 = (j1 * t1^2) * t1 * 2 = d; (受到距離 d 的限制)
結果:min(t) = t1 * 4 = [ (d / 2 j1) ^ (1/3) ] * 4;
條件1:max(v) = j1 * t1^2 ≤ m; (不會受到最大速度 m 的限制)
條件2:max(a) = j1 * t1 ≤ a1; (不會受到最大加速度 a1 的限制)
(2)case 2:受到最大速度 m 的限制,即能加速到最大速度m(此種情況可認為不受距離 d 的限制,當然也可以說 m 太小),同時也不受 a1 的限制。曲線由四個抛物線片段加一段水準線段組成。
根據:1/2 * j * (t1 ^ 2) = m / 2; (受到最大速度 m 的限制)
求出:t1 = sqrt (m / j1); 以及 t2 = (d - m * t1 * 2)/m;
結果:min(t) = t1 * 4 + t2;
條件1:m * t1 * 2 ≤ d; (不會受到距離 d 的限制)
(3)case 3:受到最大加速度 a1 的限制,同時受到距離 d 的限制,是以不能加速到最大速度 m (即不會受到最大速度 m 的限制)。曲線由四個抛物線片段加上兩段斜率絕對值為 a1 的傾斜線段組成。則由下列方程:
j1 * t1 = a1; (受到 a1 的限制)
max(v) = j1 * (t1^2) + a * t3;
d = max(v) * (t1 * 2 + t3);
結果:min(t) = t1 * 4 + t3 * 2;
條件1:max(v) ≤ m; (不受到最大速度 m 的限制)
條件2:t3 ≥ 0; (關于 t3 的負數解在後面讨論)
整理上面的方程式,我們得到一個關于 t3 的一進制二次方程如下:
a1 t3^2 + [ 3 (a1^2) / j1 ] t3 + [ 2 ( a1^3 ) / ( j1^2 ) - d ] = 0;
可以根據一進制二次方程的求根公式求出上面的 t3,解有兩個,顯然應該舍棄其中為負數的根,取正數根。
【注意】這裡 t3 的被舍棄的負數解的數學和實體意義是什麼? 在給出代碼後将繼續讨論這個問題。
(4)case 4:就是前面分析過的所有運動都包括。受到 a1 的限制是以有斜線段部分,受到 m 的限制是以有水準線段部分。但不受到距離 d 的限制(即能加速到最大速度)。有:
j1 * t1 = a1; (受到最大加速度 a1 的限制)
m = j1 * (t1^2) + a * t3; (受到最大速度 m 的限制)
t2 = ( d - m * t1 * 2 - m * t3 ) / m; (不受到距離 d 的限制)
結果:min(t) = t1 * 4 + t3 * 2 + t2;
case 4 需要滿足的條件實際上不需要列出,因為如果前面的case都不滿足條件,則一定會落入case 4。這裡為了完備,我依然給出case 4需要滿足的條件:
條件1:max ( v ) / 2 = 1/2 * j1 * (t1^2) ≤ m/2; (為了能達到最大加速度a1,要有足夠的加速空間,是以 m 必須足夠大)。
條件2:m * ( t1*2 + t3 ) ≤ d; (為了達到最大速度,必須有足夠長的距離,是以 d 必須足夠大)。
/***************************************************************/
好了,現在我們已經考慮了四種 case,有沒有任何遺漏的 case (要注意如果有就意味着 WA!)?考慮下斜線段出現的條件是不是一定要達到最大加速度 a1?是的,因為如果沒有達到最大加速度 a1 就進入某個斜率小于 a1 的斜線段,那麼如果我們繼續走抛物線(因為這時速度上還有繼續加速的空間,而加速度還沒有上升到最大值 a1,是以抛物線是可繼續的),就能更快達到最大速度,是以最終使用的時間一定會更短(假設在某點有兩條岔路,一條是高速公路,一條是坑坑窪窪的土路,它們都是可選的,你選哪一條?)!
總結:注意上面的所有條件中都有等于号,等于即表示 case 和 case 之間的臨界點。上面的 case 的排序是根據編碼實作比較友善的情況,從 case 1 可以比較容易演化到後續的 case(但其他 case 之間的演化,參數之間的互相作用要稍複雜一些),例如:處于 case1 時,如果把 m 水準線向下移動(減小 m),就會從 case1 轉入 case2;如果把表示斜率的那條射線向水準方向的 t 軸方向轉動(減小 a1 ),就會從 case1 轉入 case3;或者把距離拉長(增大 d),則曲線将向上浮動,最大速度将增大,如果先遇到 m 限制,則從 case1 轉入 case2,如果先遇到 a1 限制,則從 case1 轉入 case3。如果前面的case不能符合條件,則最終一定會落入位于後面的case(這裡我依然是基于我個人的程式設計經驗和直覺印象,最好應該更嚴謹一點)。case1是最特殊也是最簡單的情況。最後的結果是一個四元函數(超過了比較容易直覺了解的次元):
min ( t ) = f (d, m, a1, j1);
可以想象根據上面的求解過程,它類似分段函數,在不同範圍内是關于不同變量的函數。
最後我們對上訴 case 給出下清單格:
CASES
起到限制作用的參數
運動組成
最短時間
case 1
d
抛物線
t1*4
case 2
m
抛物線, 水準線(勻速)
t1*4 + t2
case 3
d, a1
抛物線, 斜線(勻加速)
t1*4 + t3*2
case 4
m, a1
抛物線, 斜線(勻加速), 水準線(勻速)
t1*4 + t3*2 + t2
注意參數 j1 的用法和其他三個參數不同,它是直接應用到抛物線函數中的參數,是唯一被直接使用的參數(其他三個參數主要起到限制作用),所有 case 都會包含四個抛物線片段,是以上表中 j1 不會在“起到限制作用的參數”中列出。前面已經提到過,這是基于直覺印象的結果,我們尚未(也并無必要)從數學上去證明這一點。
最後給出該題目的代碼,實際上就是從上訴推導過程直接翻譯過來,代碼本身沒有任何難度。
ZOJ_1096_cpp
最後,這道題目的序号是1096,位于第一個 problem sets 内,可以說排序是非常靠前的,但 AC 數量目前隻有 172 ,送出數量隻有 558,可見這些資料還是反映了其“難度”,但是難度主要在于數學和實體知識基礎上,和程式設計本身,算法等技巧上倒是沒有太大關系。
【補充讨論】case3 中 t3 的負數解的數學意義。
在case 3中,求解 t3 的一進制二次方程現在提出一個問題,為什麼出現負數解,其數學和實體意義是什麼,該方程是由 d,a1,j1 (不受到 m 的限制)組成的表達式為系數。由于方程的前兩個系數必定為正數,是以其中的一個根一定是負數(如果存在解)。那麼為什麼存在負數解,它的意義是什麼?
首先,在數學上,列出該方程的前提是,t3 >=0,最終列車經過抛物線和勻加速直線運動,到達下一個站點。我們對 d,a1,j1 代入具體數值,構造出一正一負的兩個解。參數是:
a1 = 2; j1 = 2; d = 12;
這時候抛物線部分是标準抛物線 y = x^2;
可以解出 t1 = 1;
關于 t3 的方程是 t3^2 + 3 * t3 - 4 = (t3 - 1) (t3 + 4) = 0; 是以 t3 = 1 或者 t3 = -4;
可以在數學上繪制出 t3 的這兩個解的情況的 v-t 曲線,如下圖所示:
圖中紅色線條部分就是 t3 = -4 的情況。圖中的紅色箭頭表示的是積分方向。是以可見上面的曲線積分中,抛物線(t1)和斜線段(t3)之間由于積分方向不同,存在一些互相抵銷作用。進而最終能積到面積 d。這是 t3 的負數解在數學上的含義。但是在實體意義上這樣是很難了解的,因為從抛物線片段後,出現了“負時間”,即時間倒流,最終列車停下來時是出發前 4 秒中。因為向着 t 軸負方向,是以 a = dv/dt 并未發生突變。而這種情況在實體意義上比較難以了解。
為了更好了解,換一種方式,把上圖中的斜線段部分全部向 t 的正方向映射(由于做了鏡面映射,dx = -dx' 是以對應線段上的積分方向同時會被改變),進而上圖會演化成下面的圖形:
在上圖中,如果把 t3 視作正數,則意味着加速度在每個銜接點處發生突變(即列車受到無窮大作用力,或者列車品質忽略不計,可看作沒有品質沒有慣性的質點),顯然這也是超現實的。如果不考慮圖中的積分方向,則曲線形成的面積顯然比 d 大,是以圖中标示出了積分方向,實際上兩部分是互相抵銷作用(斜線部分的積分是 24,抛物線部分的積分是 -12,是以最終兩者累加結果是 d = 12)。
盡管 t3 的負數解在實體上沒有令人滿意的含義,但這就是滿足 v 的積分 = d 的數學上的另一種可能情況。
題意:給出一個八進制的小數,轉換為 10 進制小數。輸出格式是:0.d1d2d3 ... dk [8] = 0.D1D2D3 ... Dm [10];
例如對八進制小數0.75,轉換為10進制,輸出格式:0.75 [8] = 0.953125 [10]。
分析:整數的進制轉換的方法非常簡單,而這道題目是小數進制轉換,把 8 進制轉換到 10 進制的直接方法是:
Decimal = d1 * 8^(-1) + d2 * 8^(-2) + ... + dk * 8 ^(-k)
例如對 0.75 (8進制),十進制小數 = 7 / 8 + 5 / 64 = 0.963125;
但是僅僅從題目給出的樣例輸出來看,語言本身的内置資料類型 double 的精度可能已經不能滿足要求了,是以這道題目看起來還是類似大數運算一類的題目,需要借助一個數組來存儲數位。但是如果用上面的直接轉換方法從 8 進制轉換到 10 進制,用數組的方法,在編碼實作上是很不友善的。是以考慮以 2 進制小數作為中介,即先把 8 進制轉換到 2 進制小數,再轉換到 10 進制。後面我們就能看到,這樣我們就能很友善的利用數組來儲存和給出具有任意精度(取決于數組大小,當然,如果追求更高精度也會引入少許時間和空間的代價)的結果。
把 8 進制小數轉換到 2 進制小數的方法非常簡單,隻需要把8進制小數的每一位用三位二進制數表示即可,例如 0.75 [8] = 0.111 101 [2]; 設 d1 = (b1 b2 b3) [2], d2 = (b4 b5 b6) [2]:
則對應的:0.d1 d2 d3 ... dk [8] = 0.b1 b2 b3 b4 b5 b6 ... b(3k) b(3k+1) b(3k+2) [2]
這是顯然的,因為:d1 = b1 * 4 + b2 * 2 + b3,...
是以 d1 * 8^(-1) + d2 * 8^(-2) + ... + dk * 8 ^(-k) = (b1*4 + b2*2 + b3) / 8 + ... = b1/2 + b2/4 + b3/8 + ... = 0.b1b2b3b4...[2];
再把這個二進制小數轉換到 10 進制。為了精度需要,這裡我引入一個數組:
unsigned char Dec[K]; // K 是一個常數,表征精度
這個數組的意義是,如果10進制小數是 0.D1D2D3 ... Dm [10],則 Dec[i] = D(i+1); 最終的10進制小數将是這樣:
0. Dec[0] Dec[1] Dec[2] ...
列印時隻需要在前面加上“0.”字首,然後從 0 索引開始依次輸出其元素即可。
這裡必須注意到二進制小數的小數點後第 k 位的基數 (0.5 ^ k) 的一個很重要的特征,即 (0.5 ^ k) 的小數點後的位數個數是 k(之後将全部是 0)。例如:
0.5,0.25,0.125,0.0625,...
注意這個序列,b[ i + 1 ] = b[ i ] / 2; 由于末尾數永遠是5,是以每一次除以 2 都會導緻遞增一位。是以引入另一個輔助存儲空間,用于存儲 2 進制小數的從小數點後第 1 位到第 K 位的基數(K 取決于需要的精度),顯然這是一個矩陣,例如如果取 K = 6,則定義矩陣 A :
unsigned char A[6][8];
經過初始化計算後,A 的内容如下:
5, 0, 0, 0, 0, 0, 0, 0, // A[0]: 0.5
2, 5, 0, 0, 0, 0, 0, 0, // A[1]: 0.25
1, 2, 5, 0, 0, 0, 0, 0, // A[2]: 0.125
0, 6, 2, 5, 0, 0, 0, 0, // A[3]: 0.0625
0, 3, 1, 2, 5, 0, 0, 0, // A[4]: 0.03125
0, 1, 5, 6, 2, 5, 0, 0, // A[5]: 0.015625
它的右上角元素全是0,應該算是一個下三角矩陣。其意義是 A[k] 是二進制小數第 k+1 位的基數,即 A[k] = 1/2^(k+1); 小數位長度是 Length (A[k]) = k+1;
這個矩陣類似做菜時事先準備的材料,在求解之前先計算好備用。
求解過程如下,首先把結果 Dec 數組全部清零,然後對 8 進制的小數的每一位小數,當作三位二進制數,如果對應的位為 1,就把該位的基數( A[k] )逐位累加到結果數組 Dec。最後我們在從後(遠離小數點的那一側)向前處理進位即可,這個過程稱為規整,即大數算法中最後的步驟。
代碼如下:
ZOJ_1086_cpp
總結:
(1)上面的方法,引入的輔助資料是二進制小數的基數,這是因為二進制小數在數位上隻有 0 ,1 兩種可能,這樣實際上就是提供的結果就是,我們是否累加某一個基數到結果中。考慮如果我們用輔助空間存儲的直接就是 8 進制小數的基礎,則首先,我們要準備這樣的基數的代碼實作就比較麻煩(準備過程同樣是大數除以一個小整數的大數運算!!)。另一點很不便的就是每個基數的小數的位長度和所在位之間沒有直接的函數關系(而2進制小數的基數具有這樣一個直接關系),我們還需要用對應的某一位上的數字去乘以這個基數再進行累加(而二進制小數的基數直接累加即可)。當然主要的麻煩在于第一點。第二點本來就位于大數算法中的過程之中,是以倒不顯得困難。
(2)思考上面的累加過程然後規整數位,有一個累加進位的過程,但該過程是不可能使進位持續到整數部分的,即,假設一個小數的進制為 k ( k >= 2 ),則如果小數點後每一位都是最大數字(k - 1),則這個小數在無限長循環下等于1。即:
1 = 0.99999...[10] = 0.11111...[2] = 0.77777...[8];
該小數為數列的求和:
f (n) = (k-1) * (k^-1 + k^-2 + ... k ^ -n) = (1 - k^-n) ;
n 趨向無窮大時,lim f(n) = 1;
(3)題目中并沒有明确指明或者暗示我們最終結果的精度,我們如果想要得到更高精度可以把數組取得更大,同時會增加記憶體需求。是以 K 的取值需要逐漸調整然後送出去“試驗”。最初我取 K 值為 256,空間需求略大。最終代碼中取 K = 48,結果就記憶體就已經降低到了ZOL上 C 語言的典型記憶體需求(120 KB左右)。