C5.0是決策樹模型中的算法,79年由J R Quinlan發展,并提出了ID3算法,主要針對離散型屬性資料,其後又不斷的改進,形成C4.5,它在ID3基礎上增加了隊連續屬性的離散化。C5.0是C4.5應用于大資料集上的分類算法,主要在執行效率和記憶體使用方面進行了改進。
C4.5算法是ID3算法的修訂版,采用GainRatio來加以改進方法,選取有最大GainRatio的分割變量作為準則,避免ID3算法過度配适的問題。
C5.0算法則是C4.5算法的修訂版,适用于處理大資料集,采用Boosting方式提高模型準确率,又稱為BoostingTrees,在軟體上計算速度比較快,占用的記憶體資源較少。
決策樹模型,也稱規則推理模型。通過對訓練樣本的學習,建立分類規則;依據分類規則,實作對新樣本的分類;屬于有指導(監督)式的學習方法,有兩類變量:目标變量(輸出變量),屬性變量(輸入變量)。
決策樹模型與一般統計分類模型的主要差別:決策樹的分類是基于邏輯的,一般統計分類模型是基于非邏輯的。
常見的算法有CHAID、CART、Quest和C5.0。對于每一個決策要求分成的組之間的“差異”最大。各種決策樹算法之間的主要差別就是對這個“差異”衡量方式的差別。
決策樹很擅長處理非數值型資料,這與神經網絡智能處理數值型資料比較而言,就免去了很多資料預處理工作。
C5.0是經典的決策樹模型算法之一,可生成多分支的決策樹,目标變量為分類變量,使用C5.0算法可以生成決策樹或者規則集。C5.0模型根據能偶帶來的最大資訊增益的字段拆分樣本。第一次拆分确定的樣本子集随後再次拆分,通常是根據另一個字段進行拆分,這一過程重複進行指導樣本子集不能在被拆分為止。最後,重新緝拿眼最低層次的拆分,哪些對模型值沒有顯著貢獻的樣本子集被提出或者修剪。
C5.0優點:
C5.0模型在面對資料遺漏和輸入字段很多的問題時非常穩健;
C5.0模型比一些其他類型的模型易于了解,模型退出的規則有非常直覺的解釋;
C5.0也提供強大技術以提高分類的精度。
C5.0算法
C5.0算法選擇分支變量的依據:以資訊熵的下降速度作為确定最佳分支變量和分割閥值的依據。資訊熵的下降意味着資訊的不确定性下降。
資訊熵:資訊量的數學期望,是心願發出資訊前的平均不确定性,也稱先驗熵。
資訊ui(i=1,2,…r)的發生機率P(ui)組成信源數學模型,å P(ui)=1;
資訊量(機關是bit,對的底數取2):
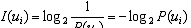
資訊熵:先驗不确定性:
•資訊熵H(U)的性質
•H(U)=0時,表示隻存在唯一的可能性,不存在不确定性
•如果信源的k個信号有相同的發出機率,即所有的ui有P(ui)=1/k, H(U)達到最大,不确定性最大
•P(ui)差别越小, H(U)就越大; P(ui) 差别大, H(U)就越小
決策樹中熵的應用:
設S是一個樣本集合,目标變量C有K個分類,freq(Ci,S)表示屬于Ci類的樣本數,|S|表示樣本幾何S的樣本數。則幾何S的資訊熵定義為:
如果某屬性變量T,有N個分類,則屬性變量T引入後的條件熵定義為:
屬性變量T帶來的資訊增益為:
C5.0算法示例:
該組樣本的熵:
關于T1的條件熵為:
T1帶來的資訊增益為: