貝葉斯分類是一類分類算法的總稱,這類算法均以貝葉斯定理為基礎,故統稱為貝葉斯分類。本文首先介紹分類問題,給出分類問題的定義。随後介紹貝葉斯分類算法的基礎——貝葉斯定理。最後介紹貝葉斯分類中最簡單的一種——樸素貝葉斯分類,并結合應用案例進一步闡釋。
對于分類問題,我們每一個人都并不陌生,因為在日常生活中我們都在或多或少地運用它。例如,當你看到一個陌生人,你的腦子下意識判斷TA是男是女;你可能經常會走在路上對身旁的朋友說“這個人一看就很有錢、那邊有個非主流”之類的話,其實這就是一種分類操作。
從數學角度來說,分類問題可做如下定義:
已知集合:
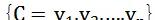
和
,确定映射規則
,使得0任意
有且僅有一個
使得
成立。其中C叫做類别集合,其中每一個元素是一個類别,而I叫做項集合,其中每一個元素是一個待分類項,f叫做分類器。分類算法的任務就是構造分類器f。
這裡要強調的是,分類問題往往采用經驗性方法構造映射規則,即一般情況下的分類問題缺少足夠的資訊來構造100%正确的映射規則,而是通過對經驗資料的學習進而實作一定機率意義上正确的分類,是以所訓練出的分類器并不是一定能将每個待分類項準确映射到其分類,分類器的品質與分類器構造方法、待分類資料的特性以及訓練樣本數量等諸多因素有關。
例如,醫生對病人進行診斷就是一個典型的分類過程,任何一個醫生都無法直接看到病人的病情,隻能觀察病人表現出的症狀和各種化驗檢測資料來推斷病情,這時醫生就好比一個分類器,而這個醫生診斷的準确率,與他當初受到的教育方式(構造方法)、病人的症狀是否突出(待分類資料的特性)以及醫生的經驗多少(訓練樣本數量)都有密切關系。
這個定了解決了現實生活裡經常遇到的問題:已知某條件機率,如何得到兩個事件交換後的機率,也就是在已知P(A|B)的情況下如何求得P(B|A)。這裡先解釋什麼是條件機率:
P(A|B)表示事件B已經發生的前提下,事件A發生的機率,叫做事件B發生下事件A的條件機率。其基本求解公式為:
貝葉斯定理之是以有用,是因為我們在生活中經常遇到這種情況:我們可以很容易直接得出P(A|B),P(B|A)則很難直接得出,但我們更關心P(B|A),貝葉斯定理就為我們打通從P(A|B)獲得P(B|A)的道路。
下面不加證明地直接給出貝葉斯定理:
樸素貝葉斯(分類器)是一種生成模型,它會基于訓練樣本對每個可能的類别模組化。之是以叫樸素貝葉斯,是因為采用了屬性條件獨立性假設,就是假設每個屬性獨立地對分類結果産生影響。即有下面的公式:
後面連乘的地方要注意的是,如果有一項機率值為0會影響後面估計,是以我們對未出現的屬性機率設定一個很小的值,并不為0,這就是拉普拉斯修正(Laplacian correction)。
拉普拉斯修正實際上假設了屬性值和類别的均勻分布,在學習過程中額外引入了先驗識。
整個樸素貝葉斯分類分為三個階段:
Stage1:準備工作階段,這個階段的任務是為樸素貝葉斯分類做必要的準備,主要工作是根據具體情況确定特征屬性,并對每個特征屬性進行适當劃分,然後由人工對一部分待分類項進行分類,形成訓練樣本集合。這一階段的輸入是所有待分類資料,輸出是特征屬性和訓練樣本。這一階段是整個樸素貝葉斯分類中唯一需要人工完成的階段,其品質對整個過程将有重要影響,分類器的品質很大程度上由特征屬性、特征屬性劃分及訓練樣本品質決定。
Stage2:分類器訓練階段,這個階段的任務就是生成分類器,主要工作是計算每個類别在訓練樣本中的出現頻率及每個特征屬性劃分對每個類别的條件機率估計,并将結果記錄。其輸入是特征屬性和訓練樣本,輸出是分類器。這一階段是機械性階段,根據前面讨論的公式可以由程式自動計算完成。
Stage3:應用階段,這個階段的任務是使用分類器對待分類項進行分類,其輸入是分類器和待分類項,輸出是待分類項與類别的映射關系。這一階段也是機械性階段,由程式完成。
在樸素的分類中,我們假定了各個屬性之間的獨立,這是為了計算友善,防止過多的屬性之間的依賴導緻的大量計算。這正是樸素的含義,雖然樸素貝葉斯的分類效果不錯,但是屬性之間畢竟是有關聯的,某個屬性依賴于另外的屬性,于是就有了半樸素貝葉斯分類器。
為了計算量不至于太大,假定每個屬性隻依賴另外的一個。這樣,更能準确描述真實情況。
公式就變成:
屬性為
所依賴的屬性,成為
的父屬性。
SOPDE方法。這種方法是假定所有的屬性都依賴于共同的一個父屬性。
TAN方法。每個屬性依賴的另外的屬性由最大帶權生成樹來确定。
先求每個屬性之間的互資訊來作為他們之間的權值。
構件完全圖。權重是剛才求得的互資訊。然後用最大帶權生成樹算法求得此圖的最大帶權的生成樹。
找一個根變量,然後依次将圖變為有向圖。
添加類别y到每個屬性的的有向邊。
三種方法的屬性依賴關系
貝葉斯算法應用舉例
以下我們再舉一些實際例子來說明貝葉斯方法被運用的普遍性,這裡主要集中在機器學習方面。
2.1 中文分詞
Google 研究員吳軍在《數學之美》系列中就有一篇是介紹中文分詞的,這裡隻介紹一下核心的思想。
分詞問題的描述為:給定一個句子(字串),如:南京市長江大橋。如何對這個句子進行分詞(詞串)才是最靠譜的。例如:
南京市/長江大橋
南京/市長/江大橋
這兩個分詞,到底哪個更靠譜呢?
我們用貝葉斯公式來形式化地描述這個問題,令 X 為字串(句子),Y 為詞串(一種特定的分詞假設)。我們就是需要尋找使得 P(Y|X) 最大的 Y ,使用一次貝葉斯可得:
用自然語言來說就是這種分詞方式(詞串)的可能性乘這個詞串生成我們的句子的可能性。我們進一步容易看到:可以近似地将 P(X|Y) 看作是恒等于 1 的,因為任意假想的一種分詞方式之下生成我們的句子總是精準地生成的(隻需把分詞之間的分界符号扔掉即可)。于是,我們就變成了去最大化 P(Y) ,也就是尋找一種分詞使得這個詞串(句子)的機率最大化。而如何計算一個詞串:W1, W2, W3, W4 ..的可能性呢?
我們知道,根據聯合機率的公式展開:P(W1, W2, W3, W4 ..) = P(W1) * P(W2|W1) * P(W3|W2, W1) * P(W4|W1,W2,W3) * .. 于是我們可以通過一系列的條件機率(右式)的乘積來求整個聯合機率。然而不幸的是随着條件數目的增加(P(Wn|Wn-1,Wn-2,..,W1) 的條件有 n-1 個),資料稀疏問題也會越來越嚴重,即便語料庫再大也無法統計出一個靠譜的 P(Wn|Wn-1,Wn-2,..,W1) 來。
為了緩解這個問題,計算機科學家們一如既往地使用了“天真”假設:我們假設句子中一個詞的出現機率隻依賴于它前面的有限的 k 個詞(k 一般不超過 3,如果隻依賴于前面的一個詞,就是2元語言模型(2-gram),同理有 3-gram 、 4-gram 等),這個就是所謂的“有限地平線”假設。雖然這個假設似乎有些理想化,但結果卻表明它的結果往往是很強大的,後面要提到的樸素貝葉斯方法使用的假設跟這個精神上是完全一緻的,我們會解釋為什麼像這樣一個理想化假設能夠得到強大的結果。
目前我們隻要知道,有了這個假設,剛才那個乘積就可以改寫成: P(W1) * P(W2|W1) * P(W3|W2) * P(W4|W3) .. (假設每個詞隻依賴于它前面的一個詞)。而統計 P(W2|W1) 就不再受到資料稀疏問題的困擾了。對于我們上面提到的例子“南京市長江大橋”,如果按照自左到右的貪婪方法分詞的話,結果就成了“南京市長/江大橋”。但如果按照貝葉斯分詞的話(假設使用 3-gram),由于“南京市長”和“江大橋”在語料庫中一起出現的頻率為 0 ,這個整句的機率便會被判定為 0 。進而使得“南京市/長江大橋”這一分詞方式勝出。
2.2 貝葉斯垃圾郵件過濾器
給定一封郵件,判定它是否屬于垃圾郵件。按照先例,我們還是用D來表示這封郵件,注意D由N個單詞組成。我們用h+來表示垃圾郵件,h-表示正常郵件。問題可以形式化地描述為求:
P(h+|D) = P(h+) * P(D|h+) / P(D)
P(h-|D) = P(h-) * P(D|h-) / P(D)
其中 P(h+) 和 P(h-) 這兩個先驗機率都是很容易求出來的,隻需要計算一個郵件庫裡面垃圾郵件和正常郵件的比例就行了。然而 P(D|h+) 卻不容易求,因為 D 裡面含有 N 個單詞 d1, d2, d3, .. ,是以P(D|h+) = P(d1,d2,..,dn|h+) 。我們又一次遇到了資料稀疏性,為何這麼說呢?P(d1,d2,..,dn|h+) 就是說在垃圾郵件當中出現跟我們目前這封郵件一模一樣的一封郵件的機率是非常小的,因為每封郵件都是不同的,世界上有無窮多封郵件。這就是資料稀疏性,因為可以肯定地說,你收集的訓練資料庫不管裡面含了多少封郵件,也不可能找出一封跟目前這封一模一樣的。結果呢?我們又該如何來計算 P(d1,d2,..,dn|h+) 呢?
我們将 P(d1,d2,..,dn|h+)擴充為: P(d1|h+) * P(d2|d1, h+) * P(d3|d2,d1, h+) * .. 。這個式子想必大家并不陌生,這裡我們會使用一個更激進的假設,我們假設 di 與 di-1 是完全條件無關的,于是式子就簡化為 P(d1|h+) * P(d2|h+) * P(d3|h+) * .. 。這個就是所謂的條件獨立假設,也正是樸素貝葉斯方法的樸素之處。而計算 P(d1|h+) * P(d2|h+) * P(d3|h+) * .. 問題至此就變得簡單了,隻要統計di這個單詞在垃圾郵件中出現的頻率即可。
通過以上學習我們發現,由于無法窮舉所有可能性,貝葉斯推斷基本上不能給出肯定的結果。盡管如此,在進行大量的測試後,如果獲得的測試結果都無誤,我們也會對自己的算法很有信心(即便算法的準确性尚未确認)。事實上,随着新的測試結果出現,算法無誤的可信度也在逐漸改變。
生活中,我們經常有意或無意地運用着貝葉斯定理,從算法的角度講,如果想真正搞懂其中的原理,還需要對數理統計知識進行更加深入地學習并且不斷實踐,最終相信大家一定能夠有所收獲。
原文釋出時間為:2017-12-7
本文作者:馮葉