圖的應用很廣泛,也有很多非常有用的算法,當然也有很多待解決的問題,根據性質,圖可以分為無向圖和有向圖。本文先介紹無向圖,後文再介紹有向圖。
之是以要研究圖,是因為圖在生活中應用比較廣泛:
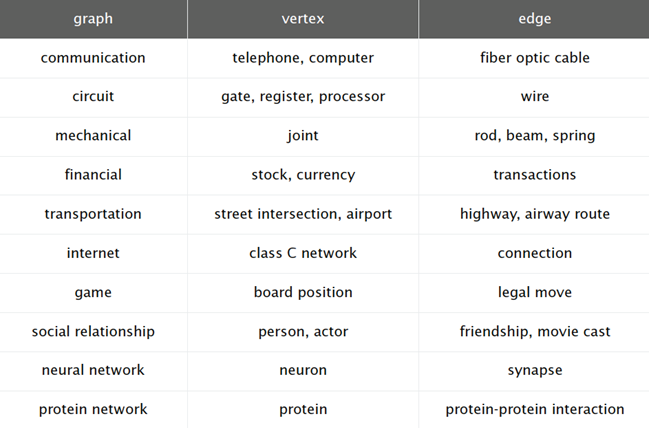
圖是若幹個頂點(Vertices)和邊(Edges)互相連接配接組成的。邊僅由兩個頂點連接配接,并且沒有方向的圖稱為無向圖。 在研究圖之前,有一些定義需要明确,下圖中表示了圖的一些基本屬性的含義,這裡就不多說明。
在研究圖之前,我們需要選用适當的資料結構來表示圖,有時候,我們常被我們的直覺欺騙,如下圖,這兩個其實是一樣的,這其實也是一個研究問題,就是如何判斷圖的形态。
要用計算機處理圖,我們可以抽象出以下的表示圖的API:
Graph的API的實作可以由多種不同的資料結構來表示,最基本的是維護一系列邊的集合,如下:
還可以使用鄰接矩陣來表示:
也可以使用鄰接清單來表示:
由于采用如上方式具有比較好的靈活性,采用鄰接清單來表示的話,可以定義如下資料結構來表示一個Graph對象。
圖也分為稀疏圖和稠密圖兩種,如下圖:
在這兩個圖中,頂點個數均為50,但是稀疏圖中隻有200個邊,稠密圖中有1000個邊。在現實生活中,大部分都是稀疏圖,即頂點很多,但是頂點的平均度比較小。
采用以上三種表示方式的效率如下:
在讨論完圖的表示之後,我們來看下在圖中比較重要的一種算法,即深度優先算法:
在談論深度優先算法之前,我們可以先看看迷宮探索問題。下面是一個迷宮和圖之間的對應關系:
迷宮中的每一個交會點代表圖中的一個頂點,每一條通道對應一個邊。
迷宮探索可以采用Trémaux繩索探索法。即:
在身後放一個繩子
通路到的每一個地方放一個繩索标記通路到的交會點和通道
當遇到已經通路過的地方,沿着繩索回退到之前沒有通路過的地方:
圖示如下:
下面是迷宮探索的一個小動畫:
深度優先搜尋算法模拟迷宮探索。在實際的圖處理算法中,我們通常将圖的表示和圖的處理邏輯分開來。是以算法的整體設計模式如下:
建立一個Graph對象
将Graph對象傳給圖算法處理對象,如一個Paths對象
然後查詢處理後的結果來擷取資訊
下面是深度優先的基本代碼,我們可以看到,遞歸調用dfs方法,在調用之前判斷該節點是否已經被通路過。
試驗一個算法最簡單的辦法是找一個簡單的例子來實作。
有了這個基礎,我們可以實作基于深度優先的路徑查詢,要實作路徑查詢,我們必須定義一個變量來記錄所探索到的路徑。
是以在上面的基礎上定義一個edgesTo變量來後向記錄所有到s的頂點的記錄,和僅記錄從目前節點到起始節點不同,我們記錄圖中的每一個節點到開始節點的路徑。為了完成這一日任務,通過設定edgesTo[w]=v,我們記錄從v到w的邊,換句話說,v-w是做後一條從s到達w的邊。 edgesTo[]其實是一個指向其父節點的樹。
上圖中是黑色線條表示 深度優先搜尋中,所有定點到原點0的路徑, 他是通過edgeTo[]這個變量記錄的,可以從右邊可以看出,他其實是一顆樹,樹根即是原點,每個子節點到樹根的路徑即是從原點到該子節點的路徑。
下圖是深度優先搜尋算法的一個簡單例子的追蹤。
通常我們更關注的是一類單源最短路徑的問題,那就是給定一個圖和一個源S,是否存在一條從s到給定定點v的路徑,如果存在,找出最短的那條(這裡最短定義為邊的條數最小)
深度優先算法是将未被通路的節點放到一個堆中(stack),雖然在上面的代碼中沒有明确在代碼中寫stack,但是 遞歸 間接的利用遞歸堆實作了這一原理。
和深度優先算法不同, 廣度優先是将所有未被通路的節點放到了隊列中。其主要原理是:
将 s放到FIFO中,并且将s标記為已通路
重複直到隊列為空
移除最近最近添加的頂點v
将v未被通路的節點添加到隊列中
标記他們為已經通路
廣度優先是以距離遞增的方式來搜尋路徑的。
廣度優先算法的搜尋步驟如下:
廣度優先搜尋首先是在距離起始點為1的範圍内的所有鄰接點中查找有沒有到達目标結點的對象,如果沒有,繼續前進在距離起始點為2的範圍内查找,依次向前推進。
本文簡要介紹了無向圖中的深度優先和廣度優先算法,這兩種算法時圖處理算法中的最基礎算法,也是後續更複雜算法的基礎。其中圖的表示,圖算法與表示的分離這種思想在後續的算法介紹中會一直沿用,下文将講解無向圖中深度優先和廣度優先的應用,以及利用這兩種基本算法解決實際問題的應用。