一、實驗目的和要求
目的:
了解線性分類器,對分類器的參數做一定的了解,了解參數設定對算法的影響。
要求:
1. 産生兩類樣本
2. 采用線性分類器生成出兩類樣本的分類面
3. 對比線性分類器的性能,對比參數設定的結果
二、實驗環境、内容和方法
環境:windows 7,matlab R2010a
内容:通過實驗,對生成的實驗資料樣本進行分類。
三、實驗基本原理
感覺器基本原理:
1.感覺器的學習過程是不斷改變權向量的輸入,更新結構中的可變參數,最後實作在有限次疊代之後的收斂。感覺器的基本模型結構如圖1所示:
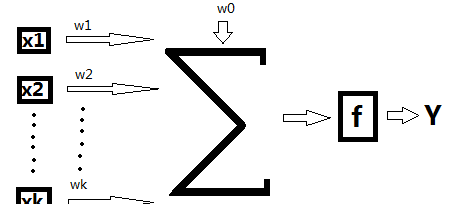
圖1 感覺器基本模型
其中,X輸入,Xi表示的是第i個輸入;Y表示輸出;W表示權向量;w0是門檻值,f是一個階躍函數。
感覺器實作樣本的線性分類主要過程是:特征向量的元素x1,x2,……,xk是網絡的輸入元素,每一個元素與相應的權wi相乘。,乘積相加後再與門檻值w0相加,結果通過f函數執行激活功能,f為系統的激活函數。因為f是一個階躍函數,故當自變量小于0時,f= -1;當自變量大于0時,f= 1。這樣,根據輸出信号Y,把相應的特征向量分到為兩類。
然而,權向量w并不是一個已知的參數,故感覺器算法很重要的一個步驟即是尋找一個合理的決策超平面。故設這個超平面為w,滿足:
(1)
引入一個代價函數,定義為:
(2)
其中,Y是權向量w定義的超平面錯誤分類的訓練向量的子集。變量
定義為:當
時,
=
-1;當
= +1。顯然,J(w)≥0。當代價函數J(w)達到最小值0時,所有的訓練向量分類都全部正确。為了計算代價函數的最小疊代值,可以采用梯度下降法設計疊代算法,即:
(3)
其中,w(n)是第n次疊代的權向量,
有多種取值方法,在本設計中采用固定非負值。由J(w)的定義,可以進一步簡化(3)得到:
(4)
通過(4)來不斷更新w,這種算法就稱為感覺器算法(perceptron algorithm)。可以證明,這種算法在經過有限次疊代之後是收斂的,也就是說,根據(4)規則修正權向量w,可以讓所有的特征向量都正确分類。
Fisher分類器原理:
Fisher線性判别分析的基本思想:通過尋找一個投影方向(線性變換,線性組合),将高維問題降低到一維問題來解決,并且要求變換後的一維資料具有如下性質:同類樣本盡可能聚集在一起,不同類的樣本盡可能地遠。
Fisher線性判别分析,就是通過給定的訓練資料,确定投影方向W和門檻值y0,即确定線性判别函數,然後根據這個線性判别函數,對測試資料進行測試,得到測試資料的類别。
1.線性投影與Fisher準則函數
在
兩類問題中,假定有
個訓練樣本
其中
個樣本來自
類型,
。兩個類型的訓練樣本分别構成訓練樣本的子集
和
。
令:
,
(4.5-1)
是向量
通過變換
得到的标量,它是一維的。實際上,對于給定的
就是判決函數的值。
由子集
的樣本映射後的兩個子集為
。因為我們關心的是
的方向,可以令
,那麼
就是
方向上的投影。使
最容易區分開的
方向正是區分超平面的法線方向。如下圖:
圖中畫出了直線的兩種選擇,圖(a)中,
還無法分開,而圖(b)的選擇可以使
區分開來。是以圖(b)的方向是一個好的選擇。
下面讨論怎樣得到最佳
方向的解析式。
各類在
維特征空間裡的樣本均值向量:
(4.5-2)
映射到一維特征空間後,各類的平均值為:
(4.5-3)
映射後,各類樣本"類内離散度"定義為:
(4.5-4)
顯然,我們希望在映射之後,兩類的平均值之間的距離越大越好,而各類的樣本類内離散度越小越好。是以,定義Fisher準則函數:
(4.5-5)
使
最大的解
就是最佳解向量,也就是Fisher的線性判别式。
2.求解
從
的表達式可知,它并非
的顯函數,必須進一步變換。
已知:
, 依次代入(4.5-1)和(4.5-2),有:
(4.5-6)
是以:
(4.5-7)
其中:
(4.5-8)
是原
維特征空間裡的樣本類内離散度矩陣,表示兩類均值向量之間的離散度大小,是以,
越大越容易區分。
将(4.5-6)
和(4.5-2)
代入(4.5-4)
式中:
(4.5-9)
(4.5-10)
是以:
(4.5-11)
顯然:
(4.5-12)
稱為原
維特征空間裡,樣本"類内離散度"矩陣。
是樣本"類内總離散度"矩陣。
為了便于分類,顯然
越小越好,也就是
越小越好。
将上述的所有推導結果代入
表達式:
—— 廣義Rayleigh商 (4.5-13)
式中
皆可由樣本集
計算出。
用lagrange乘子法求解
的極大值點。
令分母等于非零常數,也就是:
定義lagrange函數:
(4.5-14)
對
求偏導數:
令
得到:
(4.5-15)
從上述推導(4.5-10)~(4.5-12)可知,
是
維特征的樣本協方差矩陣,它是對稱的和半正定的。當樣本數目
是非奇異的,也就是可求逆。
則:
(4.5-16)
問題轉化為求一般矩陣
的特征值和特征向量。令
,則
的特征根,
的特征向量。
(4.5-17)
是一個标量。是以
總是在
方向上。将(4.5-17)代入到(4.5-15),可以得到:
其中,
是一個比例因子,不影響
的方向,可以删除,進而得到最後解:
(4.5-18)
就使
取得最大值,
可使樣本由
維空間向一維空間映射,其投影方向最好。
是一個Fisher線性判斷式。
讨論:
如果
,則樣本線性不可分。
,未必線性可分。
不可逆,未必不可分。
3.Fisher算法步驟
由Fisher線性判别式
求解向量
的步驟:
① 把來自兩類
的訓練樣本集
分成
兩個子集
② 由
,計算
③ 由
計算各類的類内離散度矩陣
④ 計算類内總離散度矩陣
⑤ 計算
的逆矩陣
⑥ 由
求解
這一節所研究的問題針對确定性模式分類器的訓練,實際上,Fisher的線性判别式對于随機模式也是适用的。
Fisher算法注釋:
(1)Fisher方法可直接求解權向量
;
(2)對線性不可分的情況,Fisher方法無法确定分類,Fisher可以進一步推廣到多類問題中去。
四、實驗過程描述
總結:
采用感覺器算法實作data1.m的資料分類流程如圖2所示:
圖2 單層感覺器算法程式流程
Fisher準則求得分類面的性能好壞一定程度上受樣本影響。有的時候Fisher可以完全正确分類,有的時候分類結果雖不是完全正确但尚可以接受,有的時候則很不理想。
五、實驗結果
感覺器分類結果:
Fisher線性分類器分類結果:
六、附錄代碼
單層感覺分類器:
function Per1()
clear
all;
close
%樣本初始化
x1(1,1)=5.1418; x1(1,2)=0.5950;
x1(2,1)=5.5519; x1(2,2)=3.5091;
x1(3,1)=5.3836; x1(3,2)=2.8033;
x1(4,1)=3.2419; x1(4,2)=3.7278;
x1(5,1)=4.4427; x1(5,2)=3.8981;
x1(6,1)=4.9111; x1(6,2)=2.8710;
x1(7,1)=2.9259; x1(7,2)=3.4879;
x1(8,1)=4.2018; x1(8,2)=2.4973;
x1(9,1)=4.7629; x1(9,2)=2.5163;
x1(10,1)=2.7118; x1(10,2)=2.4264;
x1(11,1)=3.0470; x1(11,2)=1.5699;
x1(12,1)=4.7782; x1(12,2)=3.3504;
x1(13,1)=3.9937; x1(13,2)=4.8529;
x1(14,1)=4.5245; x1(14,2)=2.1322;
x1(15,1)=5.3643; x1(15,2)=2.2477;
x1(16,1)=4.4820; x1(16,2)=4.0843;
x1(17,1)=3.2129; x1(17,2)=3.0592;
x1(18,1)=4.7520; x1(18,2)=5.3119;
x1(19,1)=3.8331; x1(19,2)=0.4484;
x1(20,1)=3.1838; x1(20,2)=1.4494;
x1(21,1)=6.0941; x1(21,2)=1.8544;
x1(22,1)=4.0802; x1(22,2)=6.2646;
x1(23,1)=3.0627; x1(23,2)=3.6474;
x1(24,1)=4.6357; x1(24,2)=2.3344;
x1(25,1)=5.6820; x1(25,2)=3.0450;
x1(26,1)=4.5936; x1(26,2)=2.5265;
x1(27,1)=4.7902; x1(27,2)=4.4668;
x1(28,1)=4.1053; x1(28,2)=3.0274;
x1(29,1)=3.8414; x1(29,2)=4.2269;
x1(30,1)=4.8709; x1(30,2)=4.0535;
x1(31,1)=3.8052; x1(31,2)=2.6531;
x1(32,1)=4.0755; x1(32,2)=2.8295;
x1(33,1)=3.4734; x1(33,2)=3.1919;
x1(34,1)=3.3145; x1(34,2)=1.8009;
x1(35,1)=3.7316; x1(35,2)=2.6421;
x1(36,1)=2.8117; x1(36,2)=2.8658;
x1(37,1)=4.2486; x1(37,2)=1.4651;
x1(38,1)=4.1025; x1(38,2)=4.4063;
x1(39,1)=3.9590; x1(39,2)=1.3024;
x1(40,1)=1.7524; x1(40,2)=1.9339;
x1(41,1)=3.4892; x1(41,2)=1.2457;
x1(42,1)=4.2492; x1(42,2)=4.5982;
x1(43,1)=4.3692; x1(43,2)=1.9794;
x1(44,1)=4.1792; x1(44,2)=0.4113;
x1(45,1)=3.9627; x1(45,2)=4.2198;
x2(1,1)=9.7302; x2(1,2)=5.5080;
x2(2,1)=8.8067; x2(2,2)=5.1319;
x2(3,1)=8.1664; x2(3,2)=5.2801;
x2(4,1)=6.9686; x2(4,2)=4.0172;
x2(5,1)=7.0973; x2(5,2)=4.0559;
x2(6,1)=9.4755; x2(6,2)=4.9869;
x2(7,1)=9.3809; x2(7,2)=5.3543;
x2(8,1)=7.2704; x2(8,2)=4.1053;
x2(9,1)=8.9674; x2(9,2)=5.8121;
x2(10,1)=8.2606; x2(10,2)=5.1095;
x2(11,1)=7.5518; x2(11,2)=7.7316;
x2(12,1)=7.0016; x2(12,2)=5.4111;
x2(13,1)=8.3442; x2(13,2)=3.6931;
x2(14,1)=5.8173; x2(14,2)=5.3838;
x2(15,1)=6.1123; x2(15,2)=5.4995;
x2(16,1)=10.4188; x2(16,2)=4.4892;
x2(17,1)=7.9136; x2(17,2)=5.2349;
x2(18,1)=11.1547; x2(18,2)=4.4022;
x2(19,1)=7.7080; x2(19,2)=5.0208;
x2(20,1)=8.2079; x2(20,2)=5.4194;
x2(21,1)=9.1078; x2(21,2)=6.1911;
x2(22,1)=7.7857; x2(22,2)=5.7712;
x2(23,1)=7.3740; x2(23,2)=2.3558;
x2(24,1)=9.7184; x2(24,2)=5.2854;
x2(25,1)=6.9559; x2(25,2)=5.8261;
x2(26,1)=8.9691; x2(26,2)=4.9919;
x2(27,1)=7.3872; x2(27,2)=5.8584;
x2(28,1)=8.8922; x2(28,2)=5.7748;
x2(29,1)=9.0175; x2(29,2)=6.3059;
x2(30,1)=7.0041; x2(30,2)=6.2315;
x2(31,1)=8.6396; x2(31,2)=5.9586;
x2(32,1)=9.2394; x2(32,2)=3.3455;
x2(33,1)=6.7376; x2(33,2)=4.0096;
x2(34,1)=8.4345; x2(34,2)=5.6852;
x2(35,1)=7.9559; x2(35,2)=4.0251;
x2(36,1)=6.5268; x2(36,2)=4.3933;
x2(37,1)=7.6699; x2(37,2)=5.6868;
x2(38,1)=7.8075; x2(38,2)=5.0200;
x2(39,1)=6.6997; x2(39,2)=6.0638;
x2(40,1)=5.6549; x2(40,2)=3.6590;
x2(41,1)=6.9086; x2(41,2)=5.4795;
x2(42,1)=7.9933; x2(42,2)=3.3660;
x2(43,1)=5.9318; x2(43,2)=3.5573;
x2(44,1)=9.5157; x2(44,2)=5.2938;
x2(45,1)=7.2795; x2(45,2)=4.8596;
x2(46,1)=5.5233; x2(46,2)=3.8697;
x2(47,1)=8.1331; x2(47,2)=4.7075;
x2(48,1)=9.7851; x2(48,2)=4.4175;
x2(49,1)=8.0636; x2(49,2)=4.1037;
x2(50,1)=8.1944; x2(50,2)=5.2486;
x2(51,1)=7.9677; x2(51,2)=3.5103;
x2(52,1)=8.2083; x2(52,2)=5.3135;
x2(53,1)=9.0586; x2(53,2)=2.9749;
x2(54,1)=8.2188; x2(54,2)=5.5290;
x2(55,1)=8.9064; x2(55,2)=5.3435;
for i=1:45 r1(i)=x1(i,1);end;
for i=1:45 r2(i)=x1(i,2);end;
for i=1:55 r3(i)=x2(i,1);end;
for i=1:55 r4(i)=x2(i,2);end;
figure(1);
%plot(r1,r2,'*',r3,r4,'o');
hold
on;%保持目前的軸和圖像不被重新整理,在該圖上接着繪制下一圖
plot(r1,r2,'ro',...
'LineWidth',1,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[1 0 0],...
'MarkerSize',7);
plot(r3,r4,'bo',...
'MarkerFaceColor',[0 0 1],...
'MarkerSize',7)
x1(:,3) = 1;% 考慮到不經過原點的超平面,對x進行擴維
x2(:,3) = 1;% 使x'=[x 1],x為2維的,故加1擴為3維
%進行初始化
w = rand(3,1);% 随機給選擇向量,生成一個3維列向量
p = 1;
%p0非負正實數
ox1 = -1;% 代價函數中的變量
ox2 = 1;% 當x屬于w1時為-1,當x屬于w2時為1
s = 1;% 辨別符,當s=0時,表示疊代終止
n = 0;% 表示疊代的次數
w1 = [0;0;0];
while s
%開始疊代
J = 0;
%假設初始的分類全部正确
j = [0;0;0];
%j=ox*x
for i = 1:45
if (x1(i,:)*w)>0
%檢視x1分類是否錯誤,在x屬于w1卻被錯誤分類的情況下,w'x<0
w1 = w;
%分類正确,權向量估計不變
else
%分類錯誤
j = j + ox1*x1(i,:)';% j=ox*x。進行累積運算
J = J + ox1*x1(i,:)*w;% 感覺器代價進行累積運算
end
for i = 1:55
if (x2(i,:)*w)<0%檢視x2分類是否錯誤,在x屬于w2卻被錯誤分類的情況下,w'x>0
j = j + ox2*x2(i,:)';% j=ox*x。進行累積運算
J = J + ox2*x2(i,:)*w;% 感覺器代價進行累積運算
if J==0
%代價為0,即分類均正确
s = 0;
%終止疊代
w1 = w - p*j;% w(t+1)=w(t)-p(ox*x)進行疊代
p=p+0.1;% 調整p
n = n+1;
%疊代次數加1
w = w1;% 更新權向量估計
x = linspace(0,10,5000);% 取5000個x的點作圖
y = (-w(1)/w(2))*x-w(3)/w(2);% x*w1+y*w2+w0=0,w=[w1;w2;w0]
plot(x,y,'r');% 用紅線畫出分界面
disp(n);% 顯示疊代的次數
axis([1,12,0,8])% 設定目前圖中,x軸範圍為1-12,為y軸範圍為0-8
Fisher分類方法:
clc
N=60;
[m1,m2,X1,Y1,X2,Y2]=SampleGen(N);
%樣本産生程式
M1=[mean(X1) mean(Y1)]';
%計算均值
M2=[mean(X2) mean(Y2)]';
S1=zeros(2,2);
S2=zeros(2,2);
%save data m1 m2 X1 X2 Y1 Y2
for i=1:length(X1)
%類内離散度計算
S1=S1+(m1(:,i)-M1)*(m1(:,i)-M1)';
for i=1:length(X2)
S2=S2+(m2(:,i)-M2)*(m2(:,i)-M2)';
Sw=S1+S2;
W=(M1-M2)\Sw;
%分類面法向量計算
w0=[mean([X1 X2]) mean([Y1 Y2])]';
%w0 計算
i=min([X1 X2]):0.001:max([X1 X2]);
U=W*w0/W(2)-W(1)/W(2).*i;
plot(X1,Y1,'.',X2,Y2,'r*',i,U,'K')
legend('w1','w2','fisher')
樣本産生函數:
function [m1,m2,X1,Y1,X2,Y2] = SampleGen(N)
x = randn(1,N);
y = randn(1,N);
i1 = 1;
i2 = 1;
for i = 1:N
if x(1) < 2*y(i)
X1(i1) = x(i);
Y1(i1) = y(i);
i1 = i1 + 1;
elseif x(i) > 2*y(i)
X2(i2) = x(i)
Y2(i2) = y(i)
i2 = i2 + 1;
plot(X1,Y1,'.');
on;
plot(X2,Y2,'r*');
m1 = ones(2,length(X1));
m2 = ones(2,length(X2));
for i = 1:length(X1)
m1(1,i) = X1(i);
m1(2,i) = Y1(i);
for i = 1:length(X2)
m2(1,i) = X2(i);
m2(2,i) = Y2(i);