<a target="_blank" href="http://lincccc.blogspot.tw/2011/03/cuda-cuts-fast-graph-cuts-on-gpu_03.html">http://lincccc.blogspot.tw/2011/03/cuda-cuts-fast-graph-cuts-on-gpu_03.html</a>
現在需要代理才能通路,是以就轉載了。
Paper:V. Vineet, P. J. Narayanan. CUDA cuts: Fast graph cuts on the GPU. In Proc. CVPR Workshop, 2008.
代碼在這個大學網站的資源裡面:
<a target="_blank" href="http://cvit.iiit.ac.in/">http://cvit.iiit.ac.in/</a>
Definition & Notation:
對于一個圖 G = (V, E) ,其中 V 為節點集合,包括源點 s 和終點 t (也可以定義多個端點,其可以優化為雙頂點圖)、以及其他諸多中間節點集合 V’ ,E 為連接配接這些節點的邊,每條邊附有容量 c(u, v) 代表節點 u 通過這條邊流向節點 v 所能承受的最大流量,在具體應用中邊的容量通常等價于其能量值。Graph cut的目的在于找到圖的Min-cut,Cut将 V’ 分割為兩個部分,去掉這些邊将使舍得圖中的任意一個節點隻與 s 或 t 相連通(如下圖),而Min-cut是所有cut中邊的能量值總和最小的一個。
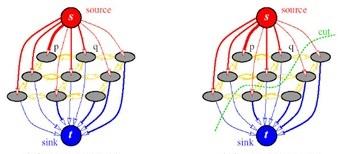
Dp 定義資料能量,Vp, q 定義平滑度能量,N 定義相鄰關系,fp 為像素 p 的标簽(屬于 s 或 t )。
經典Push-relabel算法:
Push-relabel算法,相對的,具有很強的局部性和可并行性,在每一個子操作中指關心節點及其相鄰節點。Push-relabel的基本思路是将盡可能多的流量從 s 推向 t ,但是當 t 已經無法再接受更多的流量時,這些流量将會被反推回 s,最終達到平衡(和Ford-Fulkerson算法一樣,再也找不到 s 到 t 的可用路徑)。算法過程中的“流”稱為Preflow(先流),它并不像Ford-Fulkerson算法過程中的流一樣總是持續升高直至Max-flow,而是初始預測一個值,在不斷趨近于Max-flow,過程中可能出現回流的現象。Preflow對每一個節點滿足 e(u) = in(u) – out(u),且 e(u) ≥ 0。當 e(u) > 0 時,節點 u 溢出(overflowing)。溢出的節點需要将多餘的流量Push向其相鄰的節點,即Push操作。當一條從 s 到 t 的路徑上所有的節點都不溢出時,此路徑上的Preflow就變成真正的Flow了。
Push-relabel算法和Ford-Fulkerson算法一樣都會維護一張殘餘網絡。對于圖中的每一個節點 u,若在殘餘網絡中存在 e(u, v),則 h(u) ≤ h(v) + 1。Push操作隻能在 h(u) > h(v) ,u 節點溢出且 e(u, v) 殘留容量時進行;而當 u 節點溢出,且與之相鄰所有殘留邊節點的 h(v) ≥ h(u) 時,隻能進行Label操作,增加節點 u 的高度,即 h(u) += 1。在初始化時,h(s) = n,t 及其他所有節點的高度均為 0;從 s 出發的所有邊初始化 f(e) = c(e),其餘邊 f(e) =0。Push-relabel算法将不斷重複Push和Label操作,直至任意操作都無法進行。
比較形象點,Push-relabel是泛濫的洪水,奔騰向前,堵了就倒流;Ford-Fulkerson則是很溫吞的做法,先找個人探路,回來報告能流多少水就開閘放多少。
Push-relabel算法的GPU版:
存儲和線程結構:
Grid擁有和輸入圖檔一樣的次元,并被分為若幹個Block,每個Block的次元為 B×B。每個線程對應一個節點(像素),即每個Block對應 B×B 個節點、需要通路 (B+2)×(B+2) 個節點的資料。每個節點包含以下資料:溢出量 e(u),高度 h(u),活躍狀态 flag(u) 以及與其相鄰節點間的邊的容量。活躍狀态共3種:Active,e(u) > 0 且 h(u) = h(v) + 1;Passive,e(u) > 0 且 h(u) ≠ h(v) + 1,這種狀态在Relabel後可能變成Active;Inactive,沒有溢出且沒有相鄰殘留邊,
這些資料存儲在全局或裝置記憶體中,被所有線程共享。
本文作者通過4個Kernel實作GPU版Push-relabel算法:
1) Push Kernel (node u):
■
将 h(u) 和 e(u) 從全局記憶體讀入到Block共享記憶體中(使用共享記憶體是因為一些資料會被相鄰線程共享,這種讀入方式相對單獨的讀入更節省時間);
同步線程(使用共享記憶體都需要做這一步,為了保證所有記憶體都被完全讀入了);
将 e(u) 按照Push規則推向相鄰節點(不大于邊的剩餘容量,且 h(u) ≥ h(v) );
将以上Preflow記入一個特殊的全局數組 F。
之是以記入 F,而不直接寫入相鄰節點,是因為在并行Push操作時,一個節點的溢出值同時受到多個相鄰節點的影響,如果直接寫入,可能造成資料的不一緻性(Read-after-write data consistency)。是以,作者将原來的Push操作分成了Push和Pull兩個Kernel執行(另一種選擇是在同一個Kernel中分兩部分執行,之間進行一次同步,但是對于Block邊緣的節點,這種同步需要等待其他Block的線程,這種Block間的同步并不被所有GPU支援)。
2) Pull Kernel (node u):
讀入 F 中推向 u 的Preflow;
累加所有新的Preflow,得到最終的溢出值,記入 e(u) 到全局記憶體。
3) Local Relabel Kernal (node u):
按照經典Push-relabel算法中的Relabel操作,局部地調整節點的高度
将 h(u) 和 flag(u) 從全局記憶體讀入到Block共享記憶體中;
同步線程;
計算 u 相鄰 active / passive 節點的最小高度;
該最小高度+1,作為新高度寫入 h(u) 到全局記憶體。
4) Global Relabel Kernal:
從終點 t 開始,按照廣度優先政策,周遊所有節點,更新其高度至正确的距離(節點的高度總是其與終點距離的下限)。疊代次數 k 被記錄與全局記憶體中。
如果 k == 1,所有與 t 相鄰且有殘留邊的節點高度被設為 1;
所有未被設定的節點檢查其相鄰節點,若其相鄰節點的高度為 k,則設定該節點高度為 k+1;
更新高度值到全局記憶體。
算法總體流程:
a. 計算能量矩陣 → b. Push+Pull Kernel循環 → c. Local Relabel Kernel循環 → d. Global Relabel Kernel循環 → e. 重複b到d至收斂(沒有可進行的Push和Relabel操作)
作者還基于GPU實作了Dynamic graph cut,應用于連續細微變化的Graph cut,通過對前一幀的簡單修改形成新圖,重用其他資料,加速Max-flow的求解。作者的實驗資料稱GPU實作可以提速70-100倍。不過具體應用具體分析,提速肯定是有的,多少未知,要待我實作過試驗過。據說這個印度人提供的代碼Bug頗多,雖然不太信,但還是先做了要重新實作的準備。末了,吐個槽,這論文貢獻不大,确實隻是發Workshop的水準。