假設我們有一個函數 J(w),如下圖所示。
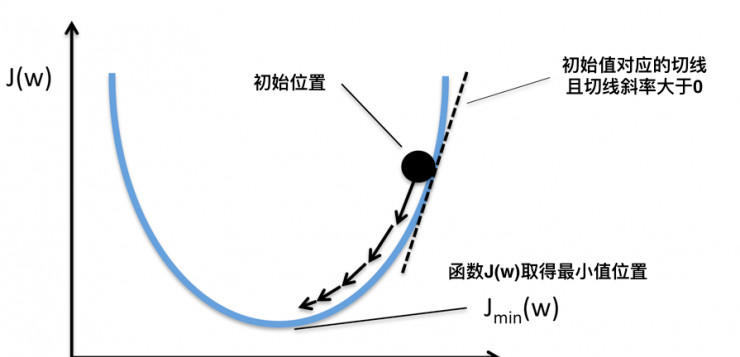
梯度下降示意圖
現在,我們要求當 w 等于什麼的時候,J(w) 能夠取到最小值。從圖中我們知道最小值在初始位置的左邊,也就意味着如果想要使 J(w) 最小,w的值需要減小。而初始位置的切線的斜率a > 0(也即該位置對應的導數大于0),w = w – a 就能夠讓 w 的值減小,循環求導更新w直到 J(w) 取得最小值。如果函數J(w)包含多個變量,那麼就要分别對不同變量求偏導來更新不同變量的值。
所謂的鍊式求導法則,就是求複合函數的導數:
鍊式求導法則
放個例題,會更加明白一點:
鍊式求導的例子
神經網絡由三部分組成,分别是最左邊的輸入層,隐藏層(實際應用中遠遠不止一層)和最右邊的輸出層。層與層之間用線連接配接在一起,每條連接配接線都有一個對應的權重值 w,除了輸入層,一般來說每個神經元還有對應的偏置 b。
神經網絡的結構圖
除了輸入層的神經元,每個神經元都會有權重求和得到的輸入值 z 和将 z 通過 Sigmoid 函數(也即是激活函數)非線性轉化後的輸出值 a,他們之間的計算公式如下
神經元輸出值 a 的計算公式
其中,公式裡面的變量l和j表示的是第 l 層的第 j 個神經元,ij 則表示從第 i 個神經元到第 j 個神經元之間的連線,w 表示的是權重,b 表示的是偏置,後面這些符号的含義大體上與這裡描述的相似,是以不會再說明。下面的 Gif 動圖可以更加清楚每個神經元輸入輸出值的計算方式(注意,這裡的動圖并沒有加上偏置,但使用中都會加上)
動圖顯示計算神經元輸出值
使用激活函數的原因是因為線性模型(無法處理線性不可分的情況)的表達能力不夠,是以這裡通常需要加入 Sigmoid 函數來加入非線性因素得到神經元的輸出值。
sigmoid 函數
可以看到 Sigmoid 函數的值域為 (0,1) ,若對于多分類任務,輸出層的每個神經元可以表示是該分類的機率。當然還存在其他的激活函數,他們的用途和優缺點也都各異。
在手工設定了神經網絡的層數,每層的神經元的個數,學習率 η(下面會提到)後,BP 算法會先随機初始化每條連接配接線權重和偏置,然後對于訓練集中的每個輸入 x 和輸出 y,BP 算法都會先執行前向傳輸得到預測值,然後根據真實值與預測值之間的誤差執行逆向回報更新神經網絡中每條連接配接線的權重和每層的偏好。在沒有到達停止條件的情況下重複上述過程。
其中,停止條件可以是下面這三條
● 權重的更新低于某個門檻值的時候 ● 預測的錯誤率低于某個門檻值 ● 達到預設一定的疊代次數
譬如說,手寫數字識别中,一張手寫數字1的圖檔儲存了28*28 = 784個像素點,每個像素點儲存着灰階值(值域為[0,255]),那麼就意味着有784個神經元作為輸入層,而輸出層有10個神經元代表數字0~9,每個神經元取值為0~1,代表着這張圖檔是這個數字的機率。
每輸入一張圖檔(也就是執行個體),神經網絡會執行前向傳輸一層一層的計算到輸出層神經元的值,根據哪個輸出神經元的值最大來預測輸入圖檔所代表的手寫數字。
然後根據輸出神經元的值,計算出預測值與真實值之間的誤差,再逆向回報更新神經網絡中每條連接配接線的權重和每個神經元的偏好。
前向傳輸(Feed-Forward)
從輸入層=>隐藏層=>輸出層,一層一層的計算所有神經元輸出值的過程。
逆向回報(Back Propagation)
因為輸出層的值與真實的值會存在誤差,我們可以用均方誤差來衡量預測值和真實值之間的誤差。
均方誤差
逆向回報的目标就是讓E函數的值盡可能的小,而每個神經元的輸出值是由該點的連接配接線對應的權重值和該層對應的偏好所決定的,是以,要讓誤差函數達到最小,我們就要調整w和b值, 使得誤差函數的值最小。
權重和偏置的更新公式
對目标函數 E 求 w 和 b 的偏導可以得到 w 和 b 的更新量,下面拿求 w 偏導來做推導。
其中 η 為學習率,取值通常為 0.1 ~ 0.3,可以了解為每次梯度所邁的步伐。注意到 w_hj 的值先影響到第 j 個輸出層神經元的輸入值a,再影響到輸出值y,根據鍊式求導法則有:
使用鍊式法則展開對權重求偏導
根據神經元輸出值 a 的定義有:
對函數 z 求 w 的偏導
Sigmoid 求導數的式子如下,從式子中可以發現其在計算機中實作也是非常的友善:
Sigmoid 函數求導
是以
則權重 w 的更新量為:
類似可得 b 的更新量為:
但這兩個公式隻能夠更新輸出層與前一層連接配接線的權重和輸出層的偏置,原因是因為 δ 值依賴了真實值y這個變量,但是我們隻知道輸出層的真實值而不知道每層隐藏層的真實值,導緻無法計算每層隐藏層的 δ 值,是以我們希望能夠利用 l+1 層的 δ 值來計算 l 層的 δ 值,而恰恰通過一些列數學轉換後可以做到,這也就是逆向回報名字的由來,公式如下:
從式子中我們可以看到,我們隻需要知道下一層的權重和神經元輸出層的值就可以計算出上一層的 δ 值,我們隻要通過不斷的利用上面這個式子就可以更新隐藏層的全部權重和偏置了。
在推導之前請先觀察下面這張圖:
l 和 l+1 層的神經元
首先我們看到 l 層的第 i 個神經元與 l+1 層的所有神經元都有連接配接,那麼我們可以将 δ 展開成如下的式子:
也即是說我們可以将 E 看做是 l+1 層所有神經元輸入值的 z 函數,而上面式子的 n 表示的是 l+1 層神經元的數量,再進行化簡後就可以得到上面所說的式子。
使用 Python 實作的神經網絡的代碼行數并不多,僅包含一個 Network 類,首先來看看該類的構造方法。
向前傳輸(FreedForward)的代碼。
源碼裡使用的是随機梯度下降(Stochastic Gradient Descent,簡稱 SGD),原理與梯度下降相似,不同的是随機梯度下降算法每次疊代隻取資料集中一部分的樣本來更新 w 和 b 的值,速度比梯度下降快,但是,它不一定會收斂到局部極小值,可能會在局部極小值附近徘徊。
根據 backprop 方法得到的偏導數更新 w 和 b 的值。
下面這塊代碼是源碼最核心的部分,也即 BP 算法的實作,包含了前向傳輸和逆向回報,前向傳輸在 Network 裡有單獨一個方法(上面提到的 feedforward 方法),那個方法是用于驗證訓練好的神經網絡的精确度的,在下面有提到該方法。
接下來則是 evaluate 的實作,調用 feedforward 方法計算訓練好的神經網絡的輸出層神經元值(也即預測值),然後比對正确值和預測值得到精确率。
最後,我們可以利用這個源碼來訓練一個手寫數字識别的神經網絡,并輸出評估的結果,代碼如下:
可以看到,在經過 30 輪的疊代後,識别手寫神經網絡的精确度在 95% 左右,當然,設定不同的疊代次數,學習率以取樣數對精度都會有影響,如何調參也是一門技術活,這個坑就後期再填吧。
神經網絡的優點:
網絡實質上實作了一個從輸入到輸出的映射功能,而數學理論已證明它具有實作任何複雜非線性映射的功能。這使得它特别适合于求解内部機制複雜的問題。
網絡能通過學習帶正确答案的執行個體集自動提取“合理的”求解規則,即具有自學習能力。
網絡具有一定的推廣、概括能力。
神經網絡的缺點:
對初始權重非常敏感,極易收斂于局部極小。
容易 Over Fitting 和 Over Training。
如何選擇隐藏層數和神經元個數沒有一個科學的指導流程,有時候感覺就是靠猜。
應用領域:
常見的有圖像分類,自動駕駛,自然語言處理等。
但其實想要訓練好一個神經網絡還面臨着很多的坑(譬如下面四條):
1. 如何選擇超參數的值,譬如說神經網絡的層數和每層的神經元數量以及學習率; 2. 既然對初始化權重敏感,那該如何避免和修正; 3. Sigmoid 激活函數在深度神經網絡中會面臨梯度消失問題該如何解決; 4. 避免 Overfitting 的 L1 和 L2正則化是什麼。
[1] 周志華 機器學習
[2] 斯坦福大學機器學習線上課程
<a href="/~jlm/papers/PDP/Volume%201/Chap8_PDP86.pdf" target="_blank">[3] Parallel Distributed Processing (1986, by David E. Rumelhart, James L. McClelland), Chapter 8 Learning Internal Representations by Error Propagation</a>
<a href="http://neuralnetworksanddeeplearning.com/chap2.%20html" target="_blank">[4] How the backpropagation algorithm works</a>
<a href="http://deeplearning.stanford.edu/wiki/index.php/Backpropagation_%20Algorithm" target="_blank">[5] Backpropagation Algorithm</a>
<a href="https://www.youtube.com/watch?v=UXF2--Ghxb0" target="_blank">[6] 鍊式求導法則,台灣中華科技大學數位課程,Youtube 視訊,順便安利一下他們的數學相關的視訊,因為做的都非常淺顯易懂</a>
====================================分割線================================
本文作者:AI研習社