此坑待埋。
點選打開漫談經典排序算法:一、從簡單選擇排序到堆排序的深度解析連結
白話經典算法系列之七 堆與堆排序
二叉排序樹與二叉堆
堆排序(注:這篇文章說明了如何從一個數組建構一個最大堆,推薦看)
最大堆的插入/删除/調整/排序操作(圖解+程式)(JAVA)
下面來說一說具體算法。
堆排序解釋第一篇(描述不太清楚)
1.堆
堆實際上是一棵完全二叉樹,其任何一非葉節點滿足性質:
Key[i]<=key[2i+1]&&Key[i]<=key[2i+2]或者Key[i]>=Key[2i+1]&&key>=key[2i+2]
即任何一非葉節點的關鍵字不大于或者不小于其左右孩子節點的關鍵字。
堆分為大頂堆和小頂堆,滿足Key[i]>=Key[2i+1]&&key>=key[2i+2]稱為大頂堆,滿足 Key[i]<=key[2i+1]&&Key[i]<=key[2i+2]稱為小頂堆。由上述性質可知大頂堆的堆頂的關鍵字肯定是所有關鍵字中最大的,小頂堆的堆頂的關鍵字是所有關鍵字中最小的。
2.堆排序的思想
利用大頂堆(小頂堆)堆頂記錄的是最大關鍵字(最小關鍵字)這一特性,使得每次從無序中選擇最大記錄(最小記錄)變得簡單。
其基本思想為(大頂堆):
1)将初始待排序關鍵字序列(R1,R2....Rn)建構成大頂堆,此堆為初始的無序區;
2)将堆頂元素R[1]與最後一個元素R[n]交換,此時得到新的無序區(R1,R2,......Rn-1)和新的有序區(Rn),且滿足R[1,2...n-1]<=R[n];
3)由于交換後新的堆頂R[1]可能違反堆的性質,是以需要對目前無序區(R1,R2,......Rn-1)調整為新堆,然後再次将R[1]與無序區最後一個元素交換,得到新的無序區(R1,R2....Rn-2)和新的有序區(Rn-1,Rn)。不斷重複此過程直到有序區的元素個數為n-1,則整個排序過程完成。
操作過程如下:
1)初始化堆:将R[1..n]構造為堆;
2)将目前無序區的堆頂元素R[1]同該區間的最後一個記錄交換,然後将新的無序區調整為新的堆。
是以對于堆排序,最重要的兩個操作就是構造初始堆和調整堆,其實構造初始堆事實上也是調整堆的過程,隻不過構造初始堆是對所有的非葉節點都進行調整。
下面舉例說明:
給定一個整形數組a[]={16,7,3,20,17,8},對其進行堆排序。
首先根據該數組元素建構一個完全二叉樹,得到
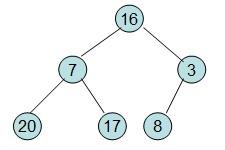
然後需要構造初始堆,則從最後一個非葉節點開始調整,調整過程如下:
20和16交換後導緻16不滿足堆的性質,是以需重新調整
這樣就得到了初始堆。
即每次調整都是從父節點、左孩子節點、右孩子節點三者中選擇最大者跟父節點進行交換(交換之後可能造成被交換的孩子節點不滿足堆的性質,是以每次交換之後要重新對被交換的孩子節點進行調整)。有了初始堆之後就可以進行排序了。
此時3位于堆頂不滿堆的性質,則需調整繼續調整
這樣整個區間便已經有序了。 從上述過程可知,堆排序其實也是一種選擇排序,是一種樹形選擇排序。隻不過直接選擇排序中,為了從R[1...n]中選擇最大記錄,需比較n-1次,然後從R[1...n-2]中選擇最大記錄需比較n-2次。事實上這n-2次比較中有很多已經在前面的n-1次比較中已經做過,而樹形選擇排序恰好利用樹形的特點儲存了部分前面的比較結果,是以可以減少比較次數。對于n個關鍵字序列,最壞情況下每個節點需比較log2(n)次,是以其最壞情況下時間複雜度為nlogn。堆排序為不穩定排序,不适合記錄較少的排序。
【ok,從一個原始數組調整成為一個堆,想必已經很清楚了,那麼如何從堆裡面擷取資料變成已經排好序的數組呢?】 下面是一個例子:
0.待排序序列:
A[6]={3,5,8,9,1,2},
1.建堆後(建堆過程參見4.4):
A[6]={9,3,8,5,1,2}
2.9和2交換,然後把9從堆中去掉後:
A[6]={2,3,8,5,1,9}
3.篩選法調整堆A[5]={2,3,8,5,1}後(調整過程參見4.3):
A[6]={8,3,2,5,1,9}
4.堆頂記錄與最後一個記錄互換,重複第二步,但是堆頂記錄和最後一個記錄的值變了
【附上另一篇文章--- 最大堆的插入/删除/調整/排序操作(圖解+程式)(JAVA)】
最大堆的插入/删除/調整/排序操作(圖解+程式)(JAVA)
堆有最大堆和最小堆之分,最大堆就是每個節點的值都>=其左右孩子(如果有的話)值的完全二叉樹。最小堆便是每個節點的值都<=其左右孩子值的完全二叉樹。
設有n個元素的序列{k1,k2,...,kn},當且僅當滿足下列關系時,稱之為堆。
堆的三種基本操作(以下以最大堆為例):
⑴最大堆的插入
由于需要維持完全二叉樹的形态,需要先将要插入的結點x放在最底層的最右邊,插入後滿 足完全二叉樹的特點;
然後把x依次向上調整到合适位置滿足堆的性質,例如下圖中插入80,先将80放在最後,然後兩次上浮到合适位置.
時間:O(logn)。 “結點上浮”
程式實作:
//向最大堆中插入元素, heap:存放堆元素的數組
public static void insert(List<Integer> heap, int value) {
//在數組的尾部添加
if(heap.size()==0)
heap.add(0);//數組下标為0的位置不放元素
heap.add(value);
//開始上升操作
// heapUp2(heap, heap.size() - 1);
heapUp(heap, heap.size() - 1);
}
//上升,讓插入的數和父節點的數值比較,當大于父節點的時候就和父節點的值相交換
public static void heapUp(List<Integer> heap, int index) {
//注意由于數值是從下标為1開始,當index = 1的時候,已經是根節點了
if (index > 1) {
//求出父親的節點
int parent = index / 2;
//擷取相應位置的數值
int parentValue = (Integer) heap.get(parent);
int indexValue = (Integer) heap.get(index);
//如果父親節點比index的數值小,就交換二者的數值
if (parentValue < indexValue) {
//交換數值
swap(heap, parent, index);
//遞歸調用
heapUp(heap, parent);
}
}
}
⑵删除
操作原理是:當删除節點的數值時,原來的位置就會出現一個孔,填充這個孔的方法就是,
把最後的葉子的值賦給該孔并下調到合适位置,最後把該葉子删除。
如圖中要删除72,先用堆中最後一個元素來35替換72,再将35下沉到合适位置,最後将葉子節點删除。
“結點下沉”
【勘誤】 大家看到上面的删除過程是不是覺得很容易明白? 我也如此認為,直到我寫程式時候出現了問題才重新審視删除算法的正确性。 譬如說:現在有一個最小堆,如下圖:
現在我選中了93,并且要删除它,接下來會發生什麼事? 接下來就是這個算法的結果了:
對,當節點沒有空間下沉的時候它就會無所事事,結果導緻不對了。 這種情況下面我們可以借用插入過程的上浮調整方式,從最下面開始向上調整。
程式:
/**
* 删除堆中位置是index處的節點
* 操作原理是:當删除節點的數值時,原來的位置就會出現一個孔
* 填充這個孔的方法就是,把最後的葉子的值賦給該孔,最後把該葉子删除
* @param heap
*/
public static void delete(List<Integer> heap,int index) {
//把最後的一個葉子的數值指派給index位置
heap.set(index, heap.get(heap.size() - 1));
//下沉操作
//heapDown2(heap, index);
heapDown(heap, index);
//把最後一個位置的數字删除
heap.remove(heap.size() - 1);
}
/**
* 遞歸實作
* 删除堆中一個資料的時候,根據堆的性質,應該把相應的位置下移,才能保持住堆性質不變
* @param heap 保持堆元素的數組
* @param index 被删除的那個節點的位置
*/
public static void heapDown(List<Integer> heap, int index) {
//因為第一個位置存儲的是空值,不在考慮之内
int n = heap.size() - 2;
//記錄最大的那個兒子節點的位置
int child = -1;
//2*index>n說明該節點沒有左右兒子節點了,那麼就傳回
if (2 * index > n) {
return;
} //如果左右兒子都存在
else if (2 * index < n) {
//定義左兒子節點
child = 2 * index;
//如果左兒子小于右兒子的數值,取右兒子的下标
if ((Integer) heap.get(child) < (Integer) heap.get(child + 1)) {
child++;
}
}//如果隻有一個兒子(左兒子節點)
else if (2 * index == n) {
child = 2 * index;
}
if ((Integer) heap.get(child) > (Integer) heap.get(index)) {
//交換堆中的child,和index位置的值
swap(heap, child, index);
//完成交換後遞歸調用,繼續下降
heapDown(heap, child);
}
}
⑶初始化
方法1:插入法:
從空堆開始,依次插入每一個結點,直到所有的結點全部插入到堆為止。
時間:O(n*log(n))
方法2:調整法:
序列對應一個完全二叉樹;從最後一個分支結點(n div 2)開始,到根(1)為止,依次對每個分支結點進行調整(下沉),
以便形成以每個分支結點為根的堆,當最後對樹根結點進行調整後,整個樹就變成了一個堆。
時間:O(n)
對如圖的序列,要使其成為堆,我們從最後一個分支結點(10/2),其值為72開始,依次對每個分支節點53,18,36 45進行調整(下沉).
【補充說明】 如何擷取相應數組序列? 方法是依次将堆的根節點的小數記下,然後删除根節點,如此反複直到堆為空。上面提到了删除操作,每次删除之後都是要調整堆讓堆的性質不變,即根節點必為最大值或最小值,明白了嗎?
程式:
/*根據樹的性質建堆,樹節點前一半一定是分支節點,即有孩子的,是以我們從這裡開始調整出初始堆*/
public static void adjust(List<Integer> heap){
for (int i = heap.size() / 2; i > 0; i--)
adjust(heap,i, heap.size()-1);
System.out.println("=================================================");
System.out.println("調整後的初始堆:");
print(heap);
}
/**
* 調整堆,使其滿足堆得定義
* @param i
* @param n
*/
public static void adjust(List<Integer> heap,int i, int n) {
int child;
for (; i <= n / 2; ) {
child = i * 2;
if(child+1<=n&&heap.get(child)<heap.get(child+1))
child+=1;/*使child指向值較大的孩子*/
if(heap.get(i)< heap.get(child)){
swap(heap,i, child);
/*交換後,以child為根的子樹不一定滿足堆定義,是以從child處開始調整*/
i = child;
} else break;
}
}
(4)最大堆排序
//對一個最大堆heap排序
public static void heapSort(List<Integer> heap) {
for (int i = heap.size()-1; i > 0; i--) {
/*把根節點跟最後一個元素交換位置,調整剩下的n-1個節點,即可排好序*/
swap(heap,1, i);
adjust(heap,1, i - 1);
}
}
(5)完整的代碼
import java.util.*;
/**
*實作的最大堆的插入和删除操作
* @author Arthur
*/
public class Heap {
/**
* 删除堆中位置是index處的值
* 操作原理是:當删除節點的數值時,原來的位置就會出現一個孔
* 填充這個孔的方法就是,把最後的葉子的值賦給該孔,最後把該葉子删除
* @param heap 一個最大堆
*/
public static void delete(List<Integer> heap,int index) {
//把最後的一個葉子的數值指派給index位置
heap.set(index, heap.get(heap.size() - 1));
//下沉操作
//heapDown2(heap, index);
heapDown(heap, index); //節點下沉
//把最後一個位置的數字删除
heap.remove(heap.size() - 1);
}
/**
* 節點下沉遞歸實作
* 删除一個堆中一個資料的時候,根據堆的性質,應該把相應的位置下移,才能保持住堆性質不變
* @param heap 保持最大堆元素的數組
* @param index 被删除的那個節點的位置
*/
public static void heapDown(List<Integer> heap, int index) {
//因為第一個位置存儲的是空值,不在考慮之内
int n = heap.size() - 2;
//記錄最大的那個兒子節點的位置
int child = -1;
//2*index>n說明該節點沒有左右兒子節點了,那麼就傳回
if (2 * index > n) {
return;
} //如果左右兒子都存在
else if (2 * index < n) {
//定義左兒子節點
child = 2 * index;
//如果左兒子小于右兒子的數值,取右兒子的下标
if ((Integer) heap.get(child) < (Integer) heap.get(child + 1)) {
child++;
}
}//如果隻有一個兒子(左兒子節點)
else if (2 * index == n) {
child = 2 * index;
}
if ((Integer) heap.get(child) > (Integer) heap.get(index)) {
//交換堆中的child,和index位置的值
swap(heap, child, index);
//完成交換後遞歸調用,繼續下降
heapDown(heap, child);
}
}
//非遞歸實作
public static void heapDown2(List<Integer> heap, int index) {
int child = 0;//存儲左兒子的位置
int temp = (Integer) heap.get(index);
int n = heap.size() - 2;
//如果有兒子的話
for (; 2 * index <= n; index = child) {
//擷取左兒子的位置
child = 2 * index;
//如果隻有左兒子
if (child == n) {
child = 2 * index;
} //如果右兒子比左兒子的數值大
else if ((Integer) heap.get(child) < (Integer) heap.get(child + 1)) {
child++;
}
//如果數值最大的兒子比temp的值大
if ((Integer) heap.get(child) >temp) {
//交換堆中的child,和index位置的值
swap(heap, child, index);
} else {
break;
}
}
}
//列印連結清單
public static void print(List<Integer> list) {
for (int i = 1; i < list.size(); i++) {
System.out.print(list.get(i) + " ");
}
System.out.println();
}
//把堆中的a,b位置的值互換
public static void swap(List<Integer> heap, int a, int b) {
//臨時存儲child位置的值
int temp = (Integer) heap.get(a);
//把index的值賦給child的位置
heap.set(a, heap.get(b));
//把原來的child位置的數值指派給index位置
heap.set(b, temp);
}
//向最大堆中插入元素
public static void insert(List<Integer> heap, int value) {
//在數組的尾部添加要插入的元素
if(heap.size()==0)
heap.add(0);//數組下标為0的位置不放元素
heap.add(value);
//開始上升操作
// heapUp2(heap, heap.size() - 1);
heapUp(heap, heap.size() - 1);
}
//節點上浮,讓插入的數和父節點的數值比較,當大于父節點的時候就和節點的值相交換
public static void heapUp(List<Integer> heap, int index) {
//注意由于數值是從小标為一開始,當index = 1的時候,已經是根節點了
if (index > 1) {
//儲存父親的節點
int parent = index / 2;
//擷取相應位置的數值
int parentValue = (Integer) heap.get(parent);
int indexValue = (Integer) heap.get(index);
//如果父親節點比index的數值小,就交換二者的數值
if (parentValue < indexValue) {
//交換數值
swap(heap, parent, index);
//遞歸調用
heapUp(heap, parent);
}
}
}
//非遞歸實作
public static void heapUp2(List<Integer> heap, int index) {
int parent = 0;
for (; index > 1; index /= 2) {
//擷取index的父節點的下标
parent = index / 2;
//獲得父節點的值
int parentValue = (Integer) heap.get(parent);
//獲得index位置的值
int indexValue = (Integer) heap.get(index);
//如果小于就交換
if (parentValue < indexValue) {
swap(heap, parent, index);
}
}
}
/*根據樹的性質建堆,樹節點前一半一定是分支節點,即有孩子的,是以我們從這裡開始調整出初始堆*/
public static void adjust(List<Integer> heap){
for (int i = heap.size() / 2; i > 0; i--)
adjust(heap,i, heap.size()-1);
System.out.println("=================================================");
System.out.println("調整後的初始堆:");
print(heap);
}
/**
* 調整堆,使其滿足堆得定義
* @param i
* @param n
*/
public static void adjust(List<Integer> heap,int i, int n) {
int child;
for (; i <= n / 2; ) {
child = i * 2;
if(child+1<=n&&heap.get(child)<heap.get(child+1))
child+=1;/*使child指向值較大的孩子*/
if(heap.get(i)< heap.get(child)){
swap(heap,i, child);
/*交換後,以child為根的子樹不一定滿足堆定義,是以從child處開始調整*/
i = child;
} else break;
}
}
//對一個最大堆heap排序
public static void heapSort(List<Integer> heap) {
for (int i = heap.size()-1; i > 0; i--) {
/*把根節點跟最後一個元素交換位置,調整剩下的n-1個節點,即可排好序*/
swap(heap,1, i);
adjust(heap,1, i - 1);
}
}
public static void main(String args[]) {
List<Integer> array = new ArrayList<Integer>(Arrays.asList(null,
1, 2, 5, 10, 3, 7, 11, 15, 17, 20, 9, 15, 8, 16));
adjust(array);//調整使array成為最大堆
delete(array,8);//堆中删除下标是8的元素
System.out.println("删除後");
print(array);
insert(array, 99);//堆中插入
print(array);
heapSort(array);//排序
System.out.println("将堆排序後:");
print(array);
System.out.println("-------------------------");
List<Integer> array1=new ArrayList<Integer>();
insert(array1,0);
insert(array1, 1);insert(array1, 2);insert(array1, 5);
insert(array1, 10);insert(array1, 3);insert(array1, 7);
insert(array1, 11);insert(array1, 15); insert(array1, 17);
insert(array1, 20);insert(array1, 9);
insert(array1, 15);insert(array1, 8);insert(array1, 16);
print(array1);
System.out.println("==============================");
array=new ArrayList<Integer>(Arrays.asList(null,45,36,18,53,72,30,48,93,15,35));
adjust(array);
insert(array, 80);//堆中插入
print(array);
delete(array,2);//堆中删除80的元素
print(array);
delete(array,2);//堆中删除72的元素
print(array);
}
}
程式運作:
D:\java>java Heap
=================================================
調整後的初始堆:
20 17 16 15 9 15 11 1 10 3 2 7 8 5
删除後
20 17 16 15 9 15 11 5 10 3 2 7 8
99 17 20 15 9 15 16 5 10 3 2 7 8 11
将堆排序後:
2 3 5 7 8 9 10 11 15 15 16 17 20 99
-------------------------
20 17 16 10 15 9 15 0 5 2 11 1 7 3 8
==============================
=================================================
調整後的初始堆:
93 72 48 53 45 30 18 36 15 35
93 80 48 53 72 30 18 36 15 35 45
93 72 48 53 45 30 18 36 15 35
93 53 48 36 45 30 18 35 15
好了,想必大家都明白了,下一篇文章将放出相關算法及結果。